Gestion du risque : la diversification
"Les éléments et parties sont complémentaires en un tout. Cette idée est triviale, plate, fausse. L'idée non triviale est : les parties sont organisées de façon complémentaire dans la constitution d'un tout. Car elle nous amène à nous interroger sur les conditions, les modalités, les limites et les problèmes que pose cette complémentarité. " Edgar Morin, La méthode.
La magie des oeufs et du panier
"Ne mets pas tous tes oeufs dans le même panier. "
Si votre grand-mére boursicote, elle doit vous l'avoir déjà dit. Sinon, vous avez sans doute lu à de multiples reprises
ce conseil de bon sens et de sagesse populaire, assorti d'une recommandation selon laquelle tout bon portefeuille se doit
de comporter au moins une dizaine de lignes différentes. Le conseil est effectivement avisé, toutefois, il est largement
simplifié et ne vous évitera pas forcément certaines déconvenues.
Maintenant que vous savez mesurer les risques, je vous propose une petite expérience de regroupement de valeurs au sein d'un portefeuille afin de voir comment se combinent les rendements des différents titres et leurs volatilités ou leurs risques.
Je me suis amusé à prendre quinze valeurs du CAC à priori non corrélées entre elles, c'est à dire appartenant à des secteurs différents. Pour laisser faire le hasard, je les ai pris en ordre alphabétique. La sélection a donc donné : Accor, AGF, Air Liquide, Alcatel, Aventis, Bouygues, Cap Gémini, Carrefour, Danone, Lafarge, Lagardère, L'Oréal, LVMH, Michelin et Pinault-Printemps-Redoute. Le tableau ci-dessous présente pour ces quinze valeurs les rendements (hors dividende) et volatilités mensuels suivants, pour les 84 mois de janvier 1993 à décembre 2000 inclus :
| Valeur | Volatilité | Rendement |
|---|---|---|
| Accor | 7,67% | 1,13% |
| AGF | 7,54% | 0,90% |
| Air Liquide | 5,60% | 0,80% |
| Alcatel | 12,66% | 2,06% |
| Aventis | 7,38% | 1,95% |
| Bouygues | 10,81% | 2,36% |
| Cap Gémini | 11,74% | 2,83% |
| Carrefour | 7,45% | 2,34% |
| Danone | 6,93% | 1,10% |
| Lafarge | 8,26% | 1,02% |
| Lagardère | 11,86% | 2,30% |
| L'Oréal | 8,11% | 2,23% |
| LVMH | 9,97% | 2,06% |
| Michelin | 8,47% | 0,67% |
| Pinault Printemps-Redoute | 8,60% | 3,06% |
| Moyenne | 8,87% | 1,79% |
Sur la même période, le CAC40 offre un rendement mensuel moyen de 1,35% avec une volatilité de 5,59%.
Le tableau ci-dessous montre l'univers des quinze titres en fonction de leur rapport rendement/risque :
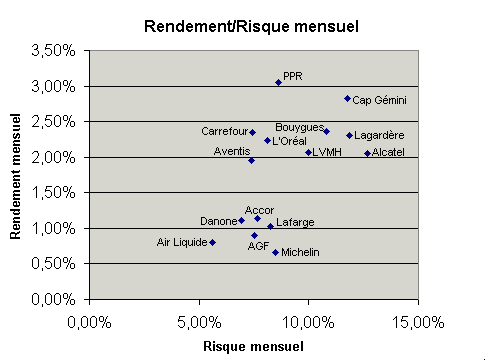
Vous pouvez constater au passage qu'Air Liquide par exemple en tant que titre de bon père de famille est le moins risqué des quinze, mais aussi le moins rémunérateur ou presque (juste supérieur à Michelin).
Ce graphique appelle une première remarque :
- les valeurs se répartissent plutôt sur un axe allant de l'origine en bas à gauche vers le coin supérieur droit,
en d'autres termes, aucune valeur ne présente de risque élevé pour un rendement faible ou de risque faible pour un
rendement élevé (rappel : il s'agit de données long terme).
Si l'on ajoute un point représentant la moyenne de volatilité et de rendement des quinze valeurs, on obtient le graphe suivant (point vert foncé) :
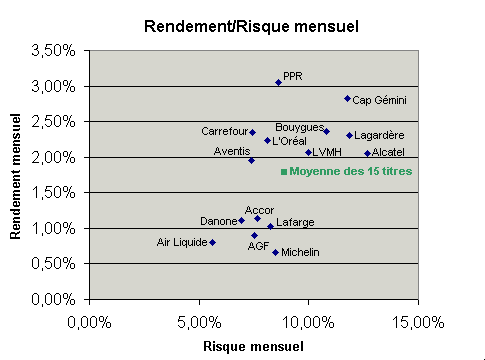
La position de la moyenne sur le graphe est conforme à nos attentes, elle se situe... dans la moyenne !
Maintenant, si l'on compose un portefeuille équipondéré des quinze valeurs et qu'on mesure son rendement et la volatilité
de ses rendements moyens mensuels, on obtient le graphe ci-dessous (point vert clair) :
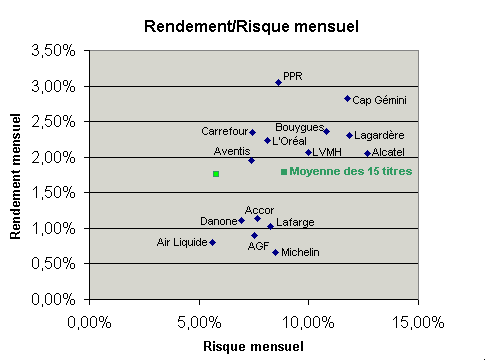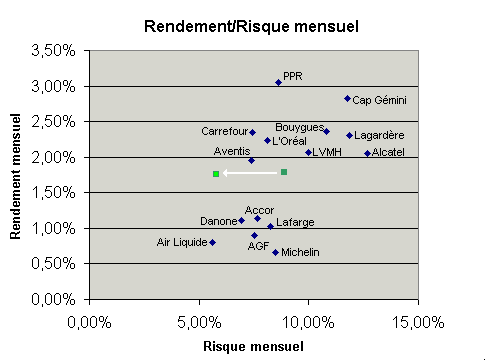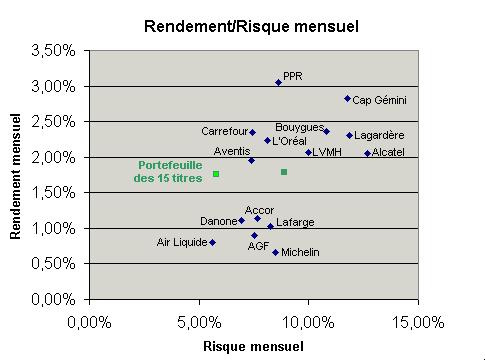
Amusant non ? Alors que le rendement d'une combinaison de titres a fortement l'air de ressembler à la moyenne arithmétique des rendements des titres qui le compose, la volatilité de cette même combinaison de titres est largement inférieure à la moyenne des volatilités des titres individuels.
La conclusion s'impose : il semble bien que l'on soit capable d'agir sur le risque, de le faire baisser sans pour autant sacrifier le rendement ! Magique non ? Et tout ceci grâce aux bienfaits de la diversification.
Pour la bonne bouche et vous permettre de voir où se situent les valeurs du CAC, le graphe ci-dessous les présente toutes, à l'exception de celles dont l'historique de cours n'est pas suffisament significatif (trop court).
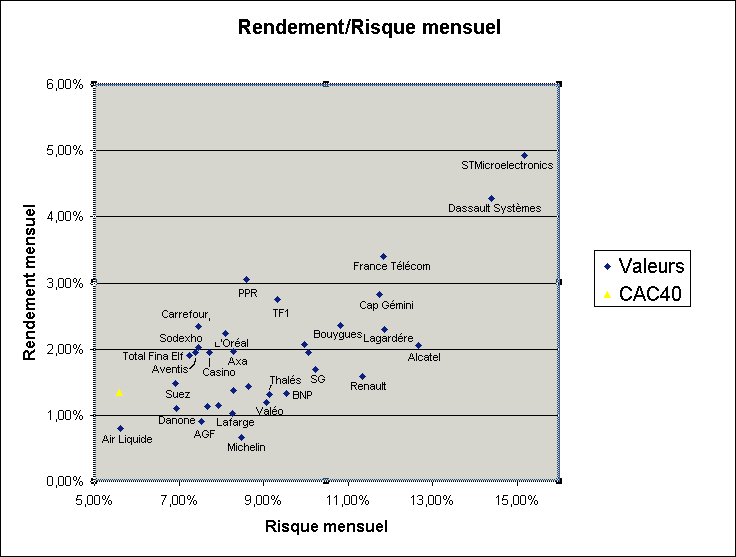
On voit encore mieux ici que les valeurs se répartissent sur la diagonale allant de (faible risque,faible rendement) à
(risque important, rendement important).
Vous noterez que le CAC40 est moins risqué que n'importe laquelle des 40 valeurs qui le compose, alors même qu'il offre un
rendement supérieur ou égal à une quinzaine d'entre elles !
Attention, les données illustrées ci-dessus portent sur un historique de plusieurs années. Plus l'horizon de temps est court,
plus la répartition des points dans l'espace rendement/risque est aléatoire.
Quoi qu'il en soit, il semble bien que le risque et le rendement soient fortement liés. 'There is no free lunch' disent les
anglo-saxons. En français : 'Il n'y a pas de repas gratuit'.
Et oui, pour gagner plus, il va probablement falloir prendre plus de risques !
Mais est-ce suffisant ? Suffit-il de prendre davantage de risques pour gagner plus ?
La corrélation
Et bien, ce n'est pas aussi simple. Résumons ce que nous avons vu jusqu'ici : on peut faire diminuer le risque par la magie
du regroupement dans la mesure où la variance d'un troupeau de titres n'est pas égale à la moyenne arithmétique des
variances de chaque titre pondérée par la proportion détenue (alors même que le rendement, lui est égal à la moyenne
arithmétique des rendements des titres individuels du troupeau).
Mais pourquoi ? Pourquoi la variance ne se comporte-t-elle pas comme le rendement ?
Et bien parce que les variations individuelles des titres du troupeau ne sont pas forcément corrélées entre elles. Si tous les titres fluctuent de la même manière, il n'y a pas de compensation, tout monte ou tout baisse. Par contre, si les titres fluctuent différemment, les hausses et les baisses se compensent partiellement. Le portefeuille fluctue alors moins que les valeurs individuelles. Et comme on assimile la variance au risque, on dit qu'il est moins risqué.
Pour illustrer ce phénomène, on peut partir d'un exemple de deux titres, A et B fictifs. La corrélation des évolutions de deux valeurs se mesure via leur covariance ou leur coefficient de corrélation. Le coefficient de corrélation est plus parlant dans la mesure où il fluctue entre -1 et 1 : 1 indique deux valeurs totalement corrélées, 0 deux valeurs dont les évolutions sont totalement indépendantes et -1 deux valeurs évoluant à l'inverse.
Dans notre exemple, si les évolutions des deux titres sont positivement corrélés, un portefeuille composé de ces deux titres fluctuera au même rythme que celui des deux valeurs qui le compose :
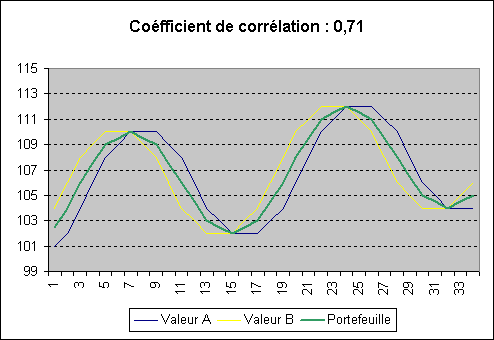
Par contre, si l'on regroupe deux titres non corrélés ou négativement corrélés entre eux (l'un descend quand l'autre monte) dans un portefeuille, les évolutions de celui-ci seront beaucoup moins heurtées :
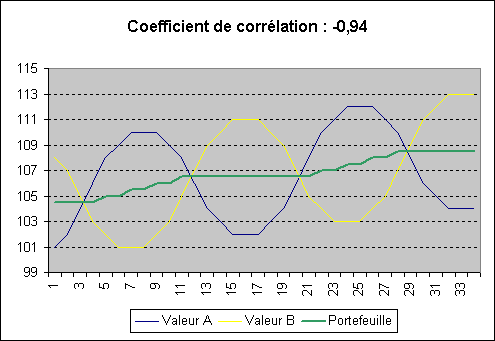
Pour diminuer le risque, il faut donc combiner au sein d'un portefeuille des valeurs si possible non corrélées entre elles.
La notion de portefeuille prend ici tout son sens. Un portefeuille n'est pas un bête amas,
tas, tombereau ou troupeau de valeurs regroupées et assemblées au hasard de coups de coeur ou idées géniales. Il s'agit
plutôt du fruit d'une construction réfléchie où chaque partie contribue à l'harmonie du tout.
Sans rire, prendre conscience de ce qui précède conduit à envisager toute opération davantage sous l'angle de sa
contribution au portefeuille, c'est à dire à l'ensemble, que sous l'angle réducteur de son rendement attendu, fut-il
diminué du risque !
Tout cela peut sembler juste emprunt d'un bon sens un peu bête, mais à bien y réfléchir, ce n'est pas aussi
trivial qu'il y paraît. Ainsi, on a plutôt naturellement tendance à faire intervenir le critère de la corrélation par exemple
uniquement au moment d'arbitrer entre plusieurs valeurs éligibles à un achat (en choisissant alors la moins corrélée au
portefeuille), c'est à dire comme critère annexe, alors qu'il devrait au contraire figurer en tête de liste de nos
critères de choix de valeurs !
Ainsi, il est par exemple préférable d'ajouter à son portefeuille une valeur non corrélée à celles déjà possédées,
plutôt qu'une autre, plus prometteuse, mais fortement corrélée à celles déjà détenues. Le rendement pourra s'en voir
amélioré et le risque diminué !
En résumé, seul le portefeuille a du sens, et...
REGLE N°2
Toute prise de position doit d'abord être considérée sous l'angle de sa contribution au portefeuille.
Maintenant, il reste à pouvoir appliquer la règle. Comment la mettre en oeuvre ?
C'est ce que nous verrons dans une prochaine partie, mais au préalable, il faut s'intéresser à la covariance...
![]() Retour au début de la page
Retour au début de la page
![]() Page suivante sur le risque
Page suivante sur le risque
![]() Retour au sommaire du risque
Retour au sommaire du risque
![]() Retour au sommaire du site
Retour au sommaire du site
Rubriques
Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse
Newsletter
Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :
Nous contacter ou nous suivre sur les réseaux
Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10