Variance d'un portefeuille

Variance passée

La variance passée d'un portefeuille peut se calculer aisément. Il suffit pour ce faire de calculer un historique des valeurs liquidatives du portefeuille, puis de calculer la variance de ses variations, comme si il s'agissait du cours d'une action. Vous pouvez pour ce faire vous référer au calcul de la variance.

Variance future

Si nous pouvions calculer avec certitude la variance future d'un portefeuille, nous serions riches. Toutefois, si cet objectif reste inaccessible, on peut par contre calculer la variance d'un portefeuille à partir de la proportion et de la variance attendue de chaque titre qui le compose.
La variance d'un portefeuille est alors donnée par la formule suivante, plus imposante que complexe, rassurez-vous :

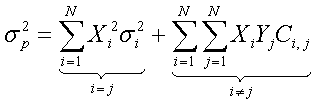
Formule de calcul de la variance d'un portefeuille

où :
X_i est la quantité de l'avoir i.
σ_i² est l'écart-type des variations de l'avoir i.
Y_j est la quantité de l'avoir j.
C_i,j est la covariance entre variations des avoir i et j.

On démontre que la variance d'un portefeuille est tout simplement la somme des covariances de tous les avoirs qui le composent, pris deux à deux et pondérées par la proportion de chaque avoir dans le portefeuille.

Pour la calculer, il suffit donc de prendre tous les avoirs du portefeuille deux à deux, de calculer leur covariance, de la multiplier par la proportion dans le portefeuille des deux avoirs et d'ajouter tous les résultats entre eux. Pour ce faire, on s'appuie en général sur une matrice de variances-covariances. La suite de cette page va vous montrer comment la construire et l'utiliser.

Matrice de variances-covariances

Le tableau ci-dessous représente une matrice de variances-covariances pour un portefeuille de n titres.

	Titre 1	Titre 2	Titre 3	...	Titre n
Titre 1	X₁² σ₁²	X₁Y₂C_1,2	X₁Y₃C_1,3	...	X₁Y_nC_1,n
Titre 2	X₂Y₁C_2,1	X₂² σ₂²	X₂Y₃C_3,3	...	X₂Y_nC_2,n
Titre 3	X₃Y₁C_3,1	X₃Y₂C_3,2	X₃² σ₃²	...	X₃Y_nC_3,n
...	...	...	...	...	...
Titre n	X_nY₁C_n,1	X₅Y₂C_5,2	X₅Y₃C_5,3	...	X_n² σ_n²

Exemple d'application

En imaginant que le portefeuille soit le suivant :

Portefeuille
Titre	Proportion
Crédit Lyonnais	10%
France Télécom	20%
Lafarge	30%
Saint-Gobain	15%
Total Fina Elf	25%

En remplaçant les proportions X_i et Y_j par leurs valeurs numériques, la matrice devient :

	Titre 1 10%	Titre 2 20%	Titre 3 30%	Titre 4 15%	Titre 5 25%
Titre 1 10%	0,1 * 0,1 * σ₁²	0,1 * 0,2 * C_1,2	0,1 * 0,3 * C_1,3	0,1 * 0,15 * C_1,4	0,1 * 0,25 * C_1,5
Titre 2 20%	0,2 * 0,1 * C_2,1	0,2 * 0,2 * σ₂²	0,2 * 0,3 * C_3,3	0,2 * 0,15 * C_2,4	0,2 * 0,25 * C_2,5
Titre 3 30%	0,3 * 0,1 * C_3,1	0,3 * 0,2 * C_3,2	0,3 * 0,3 * σ₃²	0,3 * 0,15 * C_3,4	0,3 * 0,25 * C_3,5
Titre 4 15%	0,15 * 0,1 * C_4,1	0,15 * 0,2 * C_4,2	0,15 * 0,3 * C_2,3	0,15 * 0,15 * σ₄²	0,15 * 0,25 * C_4,5
Titre 5 25%	0,25 * 0,1 * C_5,1	0,25 * 0,2 * C_5,2	0,25 * 0,3 * C_5,3	0,25 * 0,15 * C_5,4	0,25 * 0,25 * σ₅²

En prenant les variations des douze derniers mois pour base de calcul des variances-covariances :

Variations mensuelles des valeurs du portefeuille
Titre	Crédit Lyonnais	France Télécom	Lafarge	Saint-Gobain	Total Fina Elf
Août 2001	-1,75%	-32,88%	2,31%	0,31%	0,06%
Septembre 2001	-19,84%	-2,04%	-10,42%	-10,65%	-9,34%
Octobre 2001	12,28%	19,79%	10,34%	2,30%	5,76%
Novembre 2001	-3,50%	6,34%	3,85%	5,44%	-8,65%
Décembre 2001	-0,03%	1,81%	2,34%	4,05%	12,56%
Janvier 2002	-0,27%	-17,22%	-6,01%	-2,36%	1,56%
Février 2002	2,14%	-18,08%	0,91%	8,46%	4,30%
Mars 2002	14,29%	15,34%	3,02%	4,23%	4,18%
Avril 2002	7,21%	-23,23%	2,73%	1,56%	-4,97%
Mai 2002	-3,48%	-22,96%	3,70%	0,00%	-0,77%
Juin 2002	-3,94%	-54,60%	-7,51%	-4,32%	-1,50%
Juillet 2002	-8,27%	55,89%	-11,09%	-32,94%	-10,28%

Cela nous donne, une fois les variances et covariances calculées :

	Crédit Lyonnais 10%	France Télécom 20%	Lafarge 30%	Saint-Gobain 15%	Total Fina Elf 25%
Crédit Lyonnais 10%	0,1 * 0,1 * 0,0076216	0,1 * 0,2 * 0,0011506	0,1 * 0,3 * 0,0040693	0,1 * 0,15 * 0,0049138	0,1 * 0,25 * 0,0034097
France Télécom 20%	0,2 * 0,1 * 0,0011506	0,2 * 0,2 * 0,0759968	0,2 * 0,3 * -0,0006770	0,2 * 0,15 * -0,0144404	0,2 * 0,25 * -0,0028619
Lafarge 30%	0,3 * 0,1 * 0,0040693	0,3 * 0,2 * -0,0006770	0,3 * 0,3 * 0,0040396	0,3 * 0,15 * 0,0049241	0,3 * 0,25 * 0,0022138
Saint-Gobain 15%	0,15 * 0,1 * 0,0049138	0,15 * 0,2 * -0,0144404	0,15 * 0,3 * 0,0049241	0,15 * 0,15 * 0,0109851	0,15 * 0,25 * 0,0040848
Total Fina Elf 25%	0,25 * 0,1 * 0,0034097	0,25 * 0,2 * -0,0028619	0,25 * 0,3 * 0,0022138	0,25 * 0,15 * 0,0040848	0,25 * 0,25 * 0,0043380

Il nous reste alors à effectuer les calculs, puis à faire la somme des variances-covariances :

	Crédit Lyonnais 10%	France Télécom 20%	Lafarge 30%	Saint-Gobain 15%	Total Fina Elf 25%	Sous-Totaux
Crédit Lyonnais 10%	0,0000762	0,0000230	0,0001221	0,0000737	0,0000852	0,0003803
France Télécom 20%	0,0000230	0,0030399	-0,0000406	-0,0004332	-0,0001431	0,0024460
Lafarge 30%	0,0001221	-0,0000406	0,0003636	0,0002216	0,0001660	0,0008326
Saint-Gobain 15%	0,0000737	-0,0004332	0,0002216	0,0002472	0,0001532	0,0002624
Total Fina Elf 25%	0,0000852	-0,0001431	0,0001660	0,0001532	0,0002711	0,0005325
Total des variances-covariances, soit variance du portefeuille						0,0044538
Ecart-type mensuel du portefeuille = racine carrée ( variance )						0,0667365
*Ecart-type annuel du portefeuille = ecart-type PF racine carrée ( 12 )**						0,2311819

La somme des variances-covariances de chaque ligne donne la variance mensuelle du portefeuille : ici 0,0044538.
La racine carrée de cette variance est l'écart-type des variations mensuelles attendues du portefeuille, soit 0,0667365.
Si l'on souhaite obtenir l'écart-type annuel attendu des variations du portefeuille, il suffit de multiplier ce résultat par la racine carrée de 12, ce qui nous donne 0,2311819, soit 23,11% ce qui est pratiquement identique à celui du CAC40.

Vous savez maintenant calculer le risque attendu d'un portefeuille. Vous pourrez ainsi constater qu'en modifiant les proportions des différentes valeurs dans le portefeuille, on peut modifier le risque attendu du portefeuille.
Ainsi, par exemple, avec des proportions de 10%, 10%, 40%, 10% et 30% au lieu des 10%, 20%, 30%, 15% et 25% de l'exemple précédent, on obtient un portefeuille présentant un risque de 19,86% au lieu de 23,11%.

On va ainsi pouvoir jouer sur les proportions des valeurs dans le portefeuille pour essayer de baisser au maximum son risque, mais tous ces calculs sont un peu rébarbatifs. L'idéal est donc de s'en décharger sur une feuille de calcul.

Feuille de calcul de la variance future estimée d'un portefeuille

Vous pouvez télécharger le fichier excel variance_portefeuille_1.xls qui vous permettra de calculer la variance attendue d'un portefeuille de cinq titres et que vous pourrez aisément modifier pour lui faire gérer davantage de valeurs.
Cette feuille n'appelle pas de commentaires particuliers. Elle reprend les calculs réalisés dans cette page.
Les valeurs sur fond jaune clair (cours de fin de mois et proportions des valeurs dans le portefeuille) constituent les valeurs d'entrées.
Les valeurs sur fond jaune vif sont les valeurs de sortie.
La feuille Excel variance_portefeuille_2.xls est quant à elle identique à la première, mis à part le fait qu'elle comporte un historique plus important et conforme à l'échantillon minimum.

Attention !

La boule de cristal est d'une manipulation délicate

Attention, les données obtenues en sortie dépendent de celles fournies en entrée. La variance calculée sera celle du portefeuille à condition que ses composantes aient effectivement des variances telles que celles fournies en entrée, ce qui ne sera bien évidemment pas le cas. Par contre les covariances de chaque couple de valeurs ont de meilleures chances de rester stables.
Nous avons choisi ici, pour des raisons de simplicité, d'utiliser les variances passées de chaque titre en faisant comme si celles-ci ne changeaient pas dans le temps. Or, de nombreuses études ont montré que la variance (ainsi que le bêta que nous verrons plus tard peut-être) d'un titre n'est pas constante dans le temps. La variance réelle du portefeuille sera donc différente de celle calculée.

Echantillon minimum... et maximum

Tous ces calculs relèvent de la statistique, il est donc indispensable de s'appuyer sur un nombre suffisant d'observations. Ce nombre doit être au minimum d'une trentaine. Dans notre exemple nous en avons pris une douzaine pour ne pas obtenir de tableaux trop importants, il faut donc en prendre davantage.

Par ailleurs, une série de cours reflétant, au moins sur le long terme et au moins partiellement, la vie d'une entreprise, il est délicat de prendre un historique trop long car les entreprises changent avec le temps. Leur nature se modifie au fil des changements de stratégies, des fusions/acquisitions et autres événements. S'appuyer sur une durée trop longue conduirait fatalement à calculer des covariances ayant une moindre valeur prédictive.

Pour respecter ces deux contraintes, la littérature s'accorde sur le fait qu'un échantillon d'une trentaine de valeurs est suffisant, ce qui correspond pour des données mensuelles à un historique d'environ trois ans.

Un troupeau ne regroupe pas des souris et des éléphants

Les exemples utilisés dans cette page et les deux feuilles Excel téléchargeables utilisent un portefeuille de cinq titres, qui bien que relativement diversifié ne l'est pas assez. Le sujet invite à jouer sur les proportions des différentes valeurs pour voir l'impact obtenu sur le risque du troupeau, ce qui conduit souvent à affecter des proportions trop importantes à certaines valeurs, 'pour voir', et c'est légitime. Toutefois, dans la vraie vie, et au sein d'un portefeuille diversifié, la taille idéale d'une ligne est comprise entre 2 et 5% de celle du portefeuille.
Attention donc, car d'autres considérations que la volonté de réduire le risque présumé doivent être prises en compte lors de la constitution d'un portefeuille.
L'important ici est de comprendre et toucher du doigt l'importance de la covariance.

Vite, la suite...

Avec les éléments de ces quatres premières pages nous disposons de pratiquement tous les outils nécessaires à l'optimisation d'un portefeuille. On sait désormais calculer le risque attendu d'un portefeuille à partir d'une évaluation des variances futures des titres qui le composent, ainsi que son rendement à partir d'une estimation des rendements futurs des titres.
Il nous est donc maintenant possible de calculer automatiquement sa composition à partir du risque maximum acceptable tout en obtenant le rendement maximum, ou inversement à calculer automatiquement sa composition à partir du rendement souhaité et avec un risque minimum.

Je vous invite donc à poursuivre l'aventure dans une nouvelle série de pages : l'optimisation de portefeuille.

FAQ

Quelle fréquence doit-on choisir comme échantillon pour calculer la volatilité ?
Il n'y a malheureusement pas de réponse à cette question. Les valeurs les plus courantes sont une fréquence hebdomadaire sur la base des 52 dernières semaines ou bien une fréquence mensuelle sur la base des 30 derniers mois.